El objetivo de la investigación fue determinar la resistividad eléctrica de la madera de Pinus pseudostrobus, Tabebuia rosea y Quercus scytophylla en las direcciones de anisotropía. Para ello se prepararon 20 probetas de madera sólida de cada una de las especies con dimensiones de 20 mm × 20 mm × 20 mm en las direcciones radial, tangencial y longitudinal, respectivamente, y se determinó la densidad y el contenido de humedad de la madera. Para realizar las pruebas de resistividad eléctrica se midió la resistencia eléctrica empleando corriente continua con una tensión de prueba de 1000 voltios. El contenido de humedad fue para P. pseudostrobus 12,6%, para T. rosea 10,6% y para Q. scytophylla 15,6%. La resistividad eléctrica transversal promedio fue para P. pseudostrobus 45,5 MΩ m, para T. rosea 10,3 MΩ m y para Q. scytophylla 61,4 MΩ m. La resistividad eléctrica longitudinal fue para P. pseudostrobus 24,7 MΩ m, para T. rosea 2,2 MΩ m y para Q. scytophylla 19,6 MΩ m. Las magnitudes de las resistencias longitudinales medidas en las tres maderas son similares a las de las maderas reportadas en la literatura. Otro hallazgo fue que los valores de las resistividades muestran diferencias entre las direcciones de anisotropía de la madera y entre las especies estudiadas.
Palabras clave: densidad de la madera, humedad de la madera, resistencia eléctrica, corriente continua, anisotropía.
O objetivo da pesquisa foi determinar a resistividade elétrica da madeira de Pinus pseudostrobus, Tabebuia rosea e Quercus scytophylla nas direções da anisotropia. Para isso, foram preparados 20 espécimes de madeira maciça de cada uma das espécies com dimensões de 20 mm × 20 mm × 20 mm nas direções radial, tangencial e longitudinal, respectivamente, e foram determinados a densidade e o teor de umidade da madeira. Para realizar os testes de resistividade elétrica, a resistência elétrica foi medida usando corrente contínua com uma tensão de teste de 1000 volts. O conteúdo de umidade foi para P. pseudostrobus 12,6%, para T. rosea 10,6% e para Q. scytophylla 15,6%. A resistividade elétrica transversal média foi para P. pseudostrobus 45,5 MΩ m, para T. rosea 10,3 MΩ m, e para Q. scytophylla 61,4 MΩ m. A resistividade elétrica longitudinal foi para P. pseudostrobus 24,7 MΩ m, para T. rosea 2,2 MΩ m, e para Q. scytophylla 19,6 MΩ m. As magnitudes das resistências longitudinais medidas nas três madeiras são semelhantes às das madeiras relatadas na literatura. Outra constatação foi que os valores de resistividade apresentam diferenças entre as direções de anisotropia da madeira e entre as espécies estudadas.
Palavras-chave: densidade da madeira, umidade da madeira, resistência elétrica, corrente contínua, anisotropia.
Introducción
La resistividad eléctrica de la madera, también denominada resistencia eléctrica específica, es una propiedad intrínseca del material y se define como la resistencia óhmica medida en una probeta en un área de sección transversal y a una distancia definida entre electrodos y/o posiciones de aplicación de voltaje (Hafsa, et al., 2021). De tal forma que para determinar la resistividad eléctrica de la madera es necesario medir su resistencia eléctrica.
En función de los objetivos específicos de cada investigación, la literatura sobre la resistividad eléctrica de la madera reporta valores de resistencia eléctrica medidos en diferentes especies, direcciones anisotrópicas y con diferentes protocolos experimentales. Dado que la resistencia eléctrica es una característica extensiva del material, la determinación de su magnitud y el cálculo posterior de la resistividad varían ampliamente entre investigaciones.
El contenido de humedad, la especie, la anisotropía, la temperatura y la densidad son factores inherentes a la madera que afectan la determinación de su resistividad eléctrica. En el mismo sentido, las variables experimentales que modifican la medición del flujo eléctrico en la madera son las dimensiones y la forma de las probetas, la magnitud y duración del voltaje aplicado, el tipo y la configuración de los electrodos, la presión de contacto, así como los efectos electrolíticos en la pared celular del plano leñoso (Casans, et al., 2019; Hafsa, et al., 2021; Hwang, et al., 2021).
Las investigaciones donde se aplica un voltaje a una pieza de madera están principalmente orientadas hacia el estudio de alteraciones del plano leñoso. Por ejemplo, se analiza la variación de la resistencia eléctrica en la madera para varios estados de su deterioro biológico (Gao, et al., 2019). A medida que el deterioro de una pieza de madera avanza, su estructura anatómica y su composición química se modifican y la resistencia eléctrica disminuye. Este enfoque se aplica para medir la vitalidad de árboles en pie (Losso, et al., 2020), el efecto de la temperatura en la resistividad de trozas (Luo, et al., 2019), el deterioro de la madera controlado en condiciones de laboratorio (Kirker, et al., 2016), la variación de la resistencia eléctrica en madera modificada (Van Blokland y Adamopoulos, 2022) y la evaluación del estado tecnológico de madera arqueológica (Fediuk, et al., 2020).
Otro enfoque de aplicación de las propiedades eléctricas de la madera es su estudio como un biomaterial sensible, conceptualizado como un sustrato conductor para dispositivos electrónicos, por lo que podría ser una alternativa renovable a los sustratos plásticos tradicionalmente utilizados (Guo, et al., 2018; Zhang y Shen, 2019).
La escala de observación para el estudio de las propiedades eléctricas de la madera ha sido objeto de estudio, desde la tomografía de árboles en pie (Ganthaler, et al., 2019), pasando por probetas de pequeñas dimensiones (Otten, et al., 2017), hasta el nivel de la pared celular (Zelinka, et al., 2016). Para fines prácticos, cada autor mide la resistencia eléctrica en probetas con dimensiones apropiadas de acuerdo con los objetivos de sus investigaciones.
El mecanismo de conducción eléctrica en la madera depende de la presencia de iones, como portadores de carga en la pared celular, y de las propiedades de porosidad del plano leñoso, lo que resulta en un mecanismo de percolación a través del cual se produce el movimiento de iones (Zelinka, et al., 2016; Fredriksson, et al., 2021). Así, la estructura anatómica (Jiang, et al., 2003) y su composición química (Jakes, et al., 2013) juegan igualmente un papel importante en los fenómenos de transferencia del flujo eléctrico.
Una de las aplicaciones más importantes de la caracterización de las propiedades de resistencia eléctrica de la madera es la correlación con su contenido de humedad (Fernández-Golfín, et al., 2012). El paradigma vigente en ciencias de la madera propone que con la disminución del contenido de agua presente en la madera, su resistividad aumenta y, por lo tanto, la madera seca se convierte en un material aislante (Martin y Günther, 2013; Gao, et al., 2018). Este principio físico es usado en el diseño de aparatos comerciales para estimar el contenido de humedad en una pieza de madera. De tal forma que en la literatura se proponen correlaciones entre estas dos variables (Xu, et al., 2019). No obstante, estos modelos son únicamente de aplicación práctica para las especies y condiciones experimentales en las cuales fueron determinadas.
Las mediciones de resistencia eléctrica para la determinación del contenido de humedad de la madera son utilizadas en el monitoreo no destructivo de estructuras de madera (Grönquist, et al., 2021). Igualmente, las propiedades eléctricas de la madera son útiles para la caracterización y el desarrollo de materiales compuestos (Li, et al., 2020). En el mismo sentido, la resistencia eléctrica se aplica para evaluar el comportamiento de la transferencia de humedad en el rendimiento de elementos estructurales de madera expuestos al fuego (Suzuki, et al., 2021).
A pesar de su importancia tecnológica, en la literatura mexicana no se reportan valores de la resistividad eléctrica de especies endémicas de madera. El objetivo de esta investigación fue determinar la resistividad eléctrica en las direcciones radial, tangencial y longitudinal de la madera de P. pseudostrobus, T. rosea y Q. scytophylla empleando probetas de pequeñas dimensiones.
Materiales y Métodos
Se prepararon 20 probetas de madera sólida de cada una de las especies P. pseudostrobus, T. rosea y Q. scytophylla. Sus dimensiones fueron 20 mm × 20 mm × 20 mm en las direcciones radial, tangencial y longitudinal, respectivamente. La madera se almacenó en una cámara de acondicionamiento a temperatura de 20 °C y humedad relativa del aire de 65%, hasta que su peso fue constante. La densidad de la madera se determinó con la relación peso/volumen de la probeta al momento del ensayo. Después de las pruebas de resistividad eléctrica, el contenido de humedad de la madera se determinó con la diferencia de pesos al momento del ensayo y en el estado anhidro.
Las pruebas de resistividad eléctrica siguieron el siguiente protocolo: cada probeta se cepilló en sus seis caras y se posicionó entre los soportes y superficies de contacto del dispositivo fabricado para la presente investigación (Figura 1).

Figura 1. Dispositivo fabricado para las pruebas de resistividad eléctrica.
Para lograr un contacto uniforme entre la madera y las placas de cobre de 0,9 mm de espesor con resistividad eléctrica de 1,72 × 10-8 Ω m, el dispositivo aplicó presión suficiente para asegurar un flujo estable de corriente directa según la dirección y el acomodo de la probeta (Figura 2). Para cada dirección de anisotropía de la madera, se midió la resistencia eléctrica con un aparato marca Fluke, modelo 1520. En una serie de pruebas preliminares se aplicaron voltajes de 250, 500 y 1000 voltios y se observó que solo la tensión de prueba de 1000 voltios inducía mediciones de resistencia repetitivas y estables. De tal forma que se seleccionó aplicar un voltaje de 1000 voltios para las mediciones de resistencia eléctrica.
En cada prueba se realizaron tres mediciones, y con su promedio se calculó la resistividad eléctrica mediante la Ecuación 1.
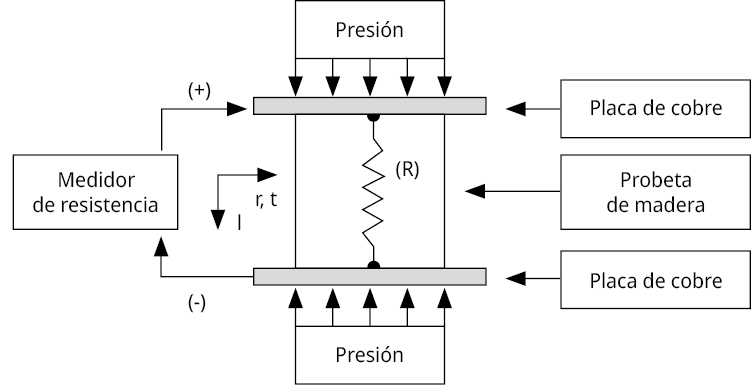
Figura 2. Configuración de las pruebas de resistividad eléctrica. R = Resistencia eléctrica; r = Dirección radial; t = Dirección tangencial; l = dirección longitudinal.
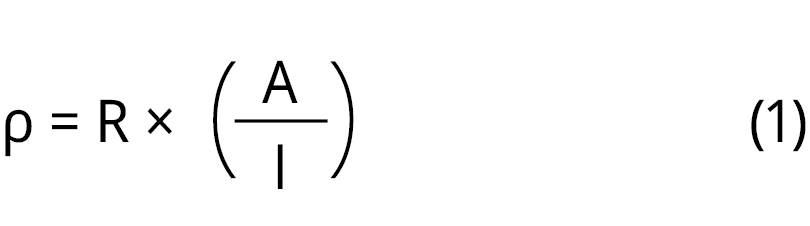
Donde:
ρ = Resistividad eléctrica (Ω m)
R = Resistencia eléctrica (Ω)
A = Área transversal a la dirección del flujo eléctrico (m2)
l = Distancia entre electrodos o puntos de aplicación del voltaje (m)
En lo subsecuente, al símbolo de la resistividad eléctrica ρ se le asocian los subíndices r, t y l para explicitar que la dirección del flujo eléctrico se midió en las direcciones radial, tangencial y longitudinal respectivamente: ρr, ρt, ρl.
Diseño experimental
Para cada especie (P. pseudostrobus, T. rosea y Q. scytophylla), la resistividad se calculó con la Ecuación 1 y se agruparon cuatro muestras: resistividad radial (ρr), resistividad tangencial (ρt), resistividad promedio radial-tangencial (Prom ρr + ρt = [(ρr + ρt) ⁄ 2]) y resistividad longitudinal (ρl). Para cada especie, los datos se compararon en pares: ρr versus ρt y Prom ρr+ρt versus ρl.
Se realizaron pruebas de normalidad de las distribuciones en cada una de las tres direcciones de anisotropía. El criterio de demarcación para considerar una distribución normal fue valores del sesgo estandarizado (SE) y apuntamiento estandarizado (AE) al interior del intervalo [-2 < SE, AE < +2]. Para estos parámetros y para la densidad (ρCH) y el contenido de humedad (CH) se determinaron su media (μ), su desviación estándar (σ) y su coeficiente de variación (CV = σ/μ).
Se realizaron pruebas de verificación y análisis de varianza con la hipótesis nula H0: σ1 = σ2 donde σ es la desviación estándar y los subíndices 1 y 2 se refieren a las muestras contrastadas. El criterio de demarcación fue valores de P(α = 0,05) ≥ 0,05, para considerar que no existe una diferencia estadísticamente significativa entre las desviaciones estándar, con un nivel del 95% de confianza.
Cuando no se cumplió con este criterio de demarcación, se realizaron pruebas de diferencias de medianas (x) de Kruskal-Wallis (K-W) con la hipótesis nula: H0: x1 = x2, donde x es la mediana y los subíndices 1 y 2 se refieren a las muestras contrastadas. Se realizaron pruebas de rangos múltiples (RM) con el criterio de demarcación de que no existen diferencias estadísticamente significativas entre aquellos niveles que comparten una misma columna de x.
Resultados y Discusión
Los valores de la densidad son comparables con los reportados por el Banco FITECMA de características físico-mecánicas de maderas mexicanas (Sotomayor, 2015): P. pseudostrobus, 540 kg m-3; T. rosea, 635 kg m-3 y Q. scytophylla, 637 kg m-3. En el mismo sentido, sus coeficientes de variación son aceptables para especies mexicanas de 10%.
El contenido de humedad de la madera varía en un intervalo de 3,9% (máximo Q. scytophylla, 14,4%, y mínimo T. rosea, 10,6%), de tal forma que se puede considerar a la madera en estado seco y con un contenido de humedad similar al alcanzado en condiciones interiores de servicio de piezas de madera. Sin embargo, los coeficientes de variación son grandes, particularmente los de T. rosea (CH = 10,6, CV = 28,8%). Dado que la resistencia eléctrica de la madera aumenta de manera exponencial cuando su contenido de humedad disminuye (Fernández-Golfín, et al., 2012; Xu, et al., 2019), este parámetro contribuyó en la variación de los resultados.
Resistencia eléctrica
La resistencia eléctrica de la madera es una característica extensiva que depende de la cantidad de materia y/o de las dimensiones del espécimen en estudio. De tal forma que es difícil comparar directamente las magnitudes reportadas en la literatura. No obstante, las magnitudes de las resistencias longitudinales medidas en P. pseudostrobus, T. rosea y Q. scytophylla son similares a las de la madera sólida de Picea abies reportadas por Slávik y otros (2019), quienes utilizaron un sistema de circuito simple de resistencia-condensador, adaptado para probetas de pequeñas dimensiones, con contenidos de humedad en el rango entre 10% y 15%. Sus condiciones son similares a las de la presente investigación ya que midieron las resistencias para distancias de 20 mm entre puntos de aplicación de la corriente eléctrica.
En el mismo contexto, Xu y otros (2019) estudiaron la variación de la resistencia eléctrica en la dirección longitudinal en madera de Liriodendron tulipifera en función de su contenido de humedad y reportaron una correlación exponencial (y = a xb) entre estas dos variables. Los valores promedio de las resistencias longitudinales de las tres maderas se posicionan relativamente bien respecto a los datos de Slávik y otros (2019), y Xu y otros (2019) (Figura 3), obtenidos con probetas de pequeñas dimensiones y en condiciones experimentales similares a las de la presente investigación.
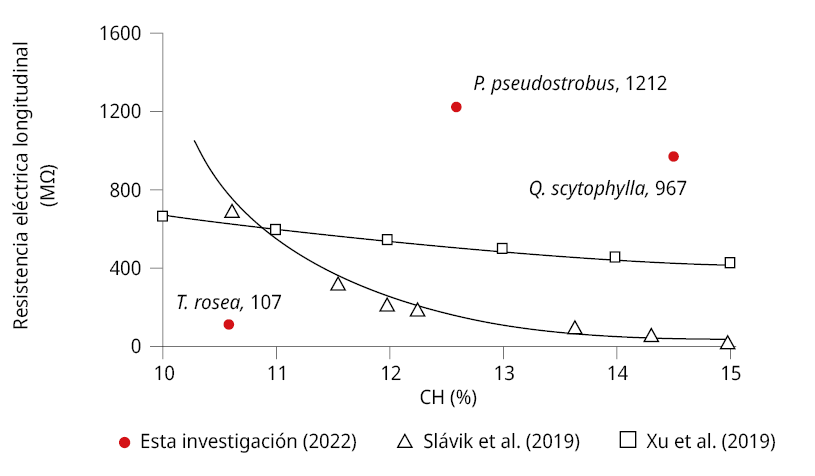
Figura 3. Posicionamiento de la resistencia eléctrica de la madera medida en la dirección longitudinal de esta investigación (2022) en comparación con datos de Slávik y otros (2019) y Xu y otros (2019).
Por su parte, Hwang y otros (2021) implementaron un experimento en el cual utilizaron placas de contacto entre el circuito que suministra la corriente eléctrica y la probeta en su sección transversal, semejante al de la presente investigación. Igualmente, estos autores emplearon un medidor de resistencia de corriente directa del mismo tipo que se utilizó en esta investigación.
Resistividad eléctrica
Los resultados de la resistividad eléctrica en las direcciones de anisotropía radial, tangencial y longitudinal de las maderas P. pseudostrobus, T. rosea y Q. scytophylla muestran valores del sesgo estandarizado y apuntamiento estandarizado al interior del intervalo [-2 < SE, AE < +2], corolarios que indican distribuciones normales (Tabla 1). Por su parte, la prueba de verificación de varianza entre las resistividades radiales y tangenciales revela que existe una diferencia significativa (P(α = 0,05) ≥ 2) entre ellas para las tres especies. Sin embargo, la prueba de verificación de varianza entre las resistencias longitudinal y el promedio medido de las resistencias radial y tangencial demuestra que para P. pseudostrobus y T. rosea existe una diferencia significativa (P(α = 0,05) ≤ 0,5), pero no existe diferencia para Q. scytophylla.
Tabla 1. Resultados del análisis estadístico de la resistividad eléctrica.
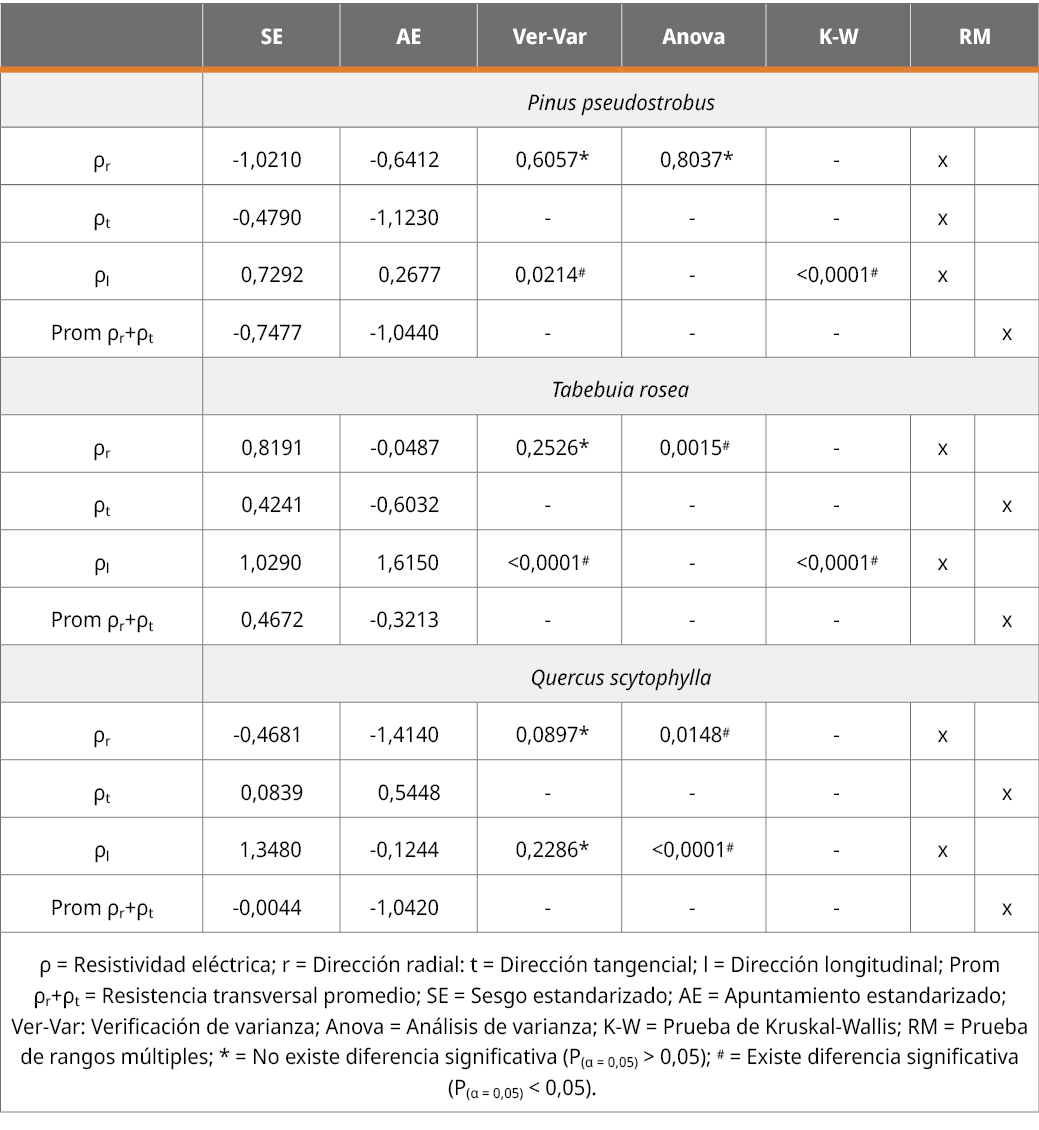
Por su parte, las pruebas de análisis de varianza entre resistividades radiales y tangenciales indican diferencias significativas para las tres maderas. Para el caso de las resistividades promedio versus las longitudinales, solamente para Q. scytophylla no existe una diferencia significativa entre estas dos variables. Para las comparaciones restantes, el análisis de varianza y las pruebas de Kruskal-Wallis indican diferencias significativas. En el mismo contexto, las pruebas de rangos múltiples distinguen los valores medios de las resistividades radiales y tangenciales, así como los promedios radial y tangencial versus longitudinal. Un caso diferente son las resistividades radiales y tangenciales de P. pseudostrobus que se agrupan sin diferencias significativas.
Los valores de las resistividades muestran diferencias entre las direcciones de anisotropía de la madera y entre las especies estudiadas (Tabla 2). Asimismo, los coeficientes de variación son altos en comparación con otras características físicas de la madera. En particular, los coeficientes de variación de la densidad de la presente investigación muestran valores aceptables para este parámetro al interior de una misma especie (Sotomayor, 2015).
Tabla 2. Densidad, contenido de humedad y resistividad eléctrica.
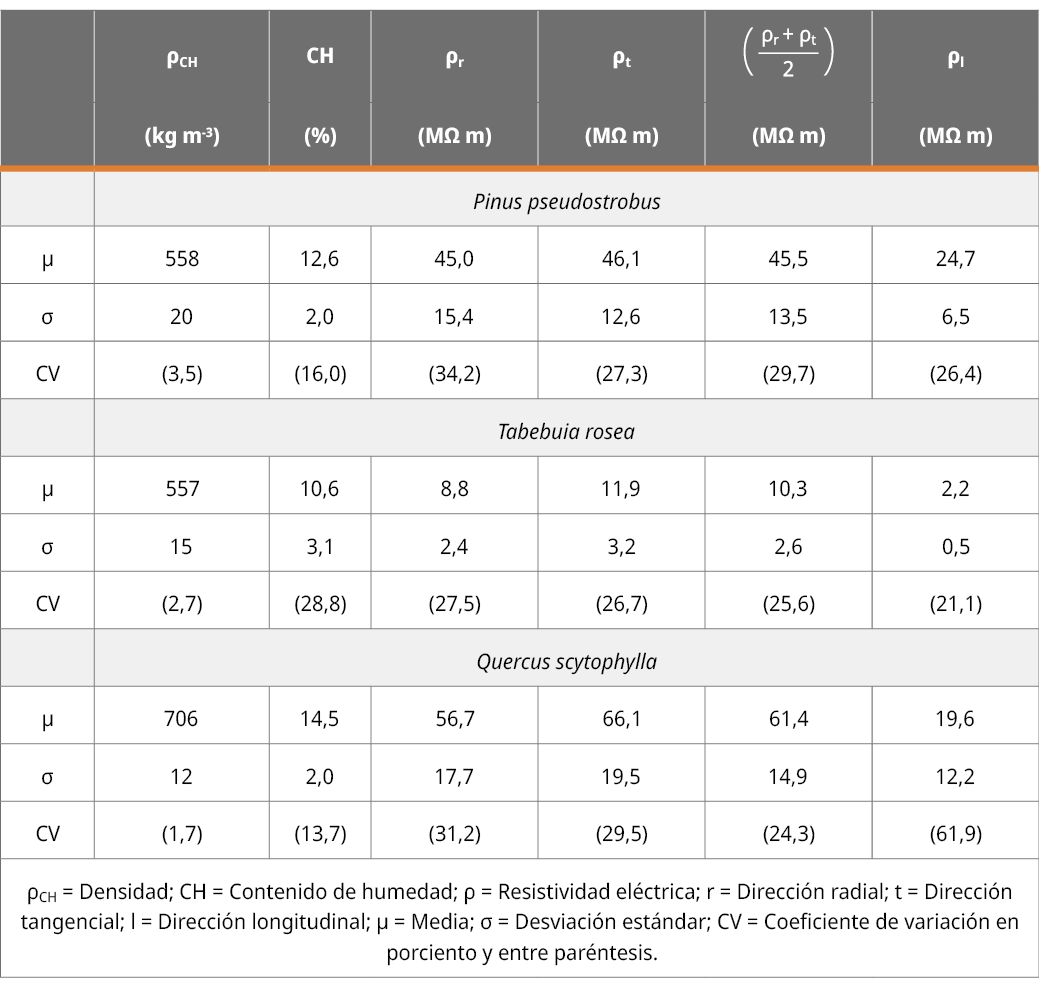
Independientemente de la magnitud de las resistividades eléctricas y la especie en cuestión, el orden de su anisotropía es en promedio: ρl / ρr = 0,55; ρl / ρt = 0,54; y si se compara la anisotropía transversal, representada por el promedio de las resistividades ρr y ρt versus la resistividad longitudinal ρl, esta anisotropía transversal-longitudinal es en promedio de 0,54, valor cercano a la anisotropía ρl/ρr. Estas estimaciones son similares a las publicados por Simpson y TenWolde (2010): ρl / ρr = 0,55; ρl / ρt = 0,50, los cuales son aceptados como referencia en tecnología de la madera.
Conclusiones
Se determinaron las resistividades eléctricas de P. pseudostrobus, T. rosea y Q. scytophylla en las direcciones radial, tangencial y longitudinal. La estrategia experimental utilizada en la presente investigación es útil para medir la resistencia eléctrica en probetas de madera de pequeñas dimensiones, lo que posteriormente permitió determinar su resistividad. La resistividad eléctrica de las maderas P. pseudostrobus, T. rosea y Q. scytophylla denota un carácter anisotrópico y una variabilidad entre las especies estudiadas.
Agradecimientos
Las pruebas de resistividad eléctrica se realizaron en el Laboratorio de Electrónica de la Facultad de Ingeniería Eléctrica de la Universidad Michoacana de San Nicolás de Hidalgo (UMSNH), Morelia, Michoacán, México. La investigación fue patrocinada por la Coordinación de la Investigación Científica de la UMSNH.
Referencias
Casans Berga, S., Garcia-Gil, R., Navarro Anton, A. E. y Rosado-Muñoz, A., 2019. Novel wood resistance measurement method reducing the initial transient instabilities arising in DC methods due to polarization effects. En: Electronics, 8(11). DOI: https://doi.org/10.3390/electronics8111253
Fediuk, A., Wilken, D., Wunderlich, T. y Rabbel, W. 2020. Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics. En: Geosciences, 10(4), 146. DOI: https://doi.org/10.3390/geosciences10040146
Fernández-Golfin, J., Conde Garcia, M., Fernández-Golfin, J. J., Calvo Haro, R., Baonza Merino, M. V. y De Palacios, P., 2012. Curves for the estimation of the moisture content of ten hardwoods by means of electrical resistance measurements. En: Forest Systems, 21(1), pp.121-127. DOI: http://dx.doi.org/10.5424/fs/2112211-11429
Fredriksson, M., Thybring, E. E. y Zelinka, S. L., 2021. Artifacts in electrical measurements on wood caused by non-uniform moisture distributions. En: Holzforschung, 75(6), pp.517-525. DOI: https://doi.org/10.1515/hf-2020-0138
Ganthaler, A., Sailer, J., Bär, A., Losso, A. y Mayr, S., 2019. Noninvasive analysis of tree stems by electrical resistivity tomography: unraveling the effects of temperature, water status, and electrode installation. En: Frontiers in Plant Science, 10. DOI: http://doi.org/10.3389/fpls.2019.01455
Gao, S., Bao, Z., Wang, L. y Yue, X., 2018. Comparison of voltammetry and digital bridge methods for electrical resistance measurements in wood. En: Computers and Electronics in Agriculture, 145, pp.161-168. DOI: https://doi.org/10.1016/j.compag.2017.11.004
Gao, S., Yue, X. y Wang, L., 2019. Effect of the degree of decay on the electrical resistance of wood degraded by brown-rot fungi. En: Canadian Journal of Forest Research, 49(2), pp.145-153. DOI: https://doi.org /10.1139/cjfr-2018-0282
Grönquist, P., Weibel, G., Leyder, C. y Frangi, A., 2021. Calibration of electrical resistance to moisture content for beech laminated veneer lumber “BauBuche S” and “BauBuche Q”. En: Forests, 12(5), 635. DOI: https://doi.org/10.3390/f12050635
Guo, H., Büchel, M., Li, X., Wäckerlin, A., Chen, Q. y Burgert, I. 2018. Dictating anisotropic electric conductivity of a transparent copper nanowire coating by the surface structure of wood. En: Journal of the Royal Society Interface, 15(142). DOI: http://doi.org/10.1098/rsif.2017.0864
Hafsa, W., Angellier, N., Takarli, M. y Pop, O. 2021. A mixed experimental-numerical electrical resistivity-based method for moisture content assessment in wood tested using the example of Douglas fir. En: Wood Science and Technology, 55(4), pp.697-718. DOI: https://doi.org/10.1007/s00226-021-01281-x
Hwang, S. W., Hwang, S. Y., Lee, T., Ahn, K. S., Pang, S. J., Park, J., Oh, J. K., Kwak, H. W. y Yeo, H., 2021. Investigation of electrical characteristics using various electrodes for evaluating the moisture content in wood. En: BioResources, 16(4), pp.7040-7055. DOI: https://doi.org/10.15376/biores.16.4.7040-7055
Jakes, J. E., Plaza, N., Stone, D. S., Hunt, C. G., Glass, S. V. y Zelinka, S. L., 2013. Mechanism of transport through wood cell wall polymers. En: Journal of Forest Products & Industries, 2(6), pp.10-13. DOI: https://www.fpl.fs.fed.us/documnts/pdf2013/fpl_2013_jakes002.pdf
Jiang, Z. H., Chen, Z., Fen, B. H., Hou Z. Q. y Chen, G. H., 2003. Modeling ovendry softwood resistivity based on the resistor network theory. En: Holzforschung, 57(4), pp.415-420. DOI: https://doi.org/10.1515/HF.2003.061
Kirker, G. T., Bishell, A. B. y Zelinka, S. L., 2016. Electrical properties of wood colonized by Gloeophyllum trabeum. En: International Biodeterioration & Biodegradation, 114, pp.110-115. DOI: http://dx.doi.org/10.1016/j.ibiod.2016.06.004
Li, J., Wang, Y., Zhang, J. y Qi, D., 2020. Physical characteristics and fluorescence effect of “environmentally friendly” metallized wood. En: AIP Advances, 10, 045133. DOI: https://doi.org/10.1063/1.5127236
Losso, A., Sailer, J., Bär, A., Ganthaler, A. y Mayr, S., 2020. Insights into trunks of Pinus cembra L.: analyses of hydraulics via electrical resistivity tomography. En: Trees, 34, pp.999-1008. DOI: https://doi.org/10.1007/s00468-020-01976-x
Luo, Z., Guan, H. y Zhang, X., 2019. The temperature effect and correction models for using electrical resistivity to estimate wood moisture variations. En: Journal of Hydrology, 578. DOI: https://doi.org/10.1016/j.jhydrol.2019.124022
Martin, T. y Günther, T., 2013. Complex resistivity tomography (CRT) for fungus detection on standing oak trees. En: European Journal of Forest Resources, 132(5-6), pp.765-776. DOI: https://doi.org/10.1007/s10342-013-0711-4
Otten, K. A., Brischke, C. y Meyer, C., 2017. Material moisture content of wood and cement mortars-Electrical resistance-based measurements in the high ohmic range. En: Construction and Building Materials, 153, pp.640-646. DOI: http://dx.doi.org/10.1016/j.conbuildmat.2017.07.090
Simpson, W. y TenWolde, A., 2010. Physical properties and moisture relations of wood. Chapter 3. En: Forest Products Laboratory. Wood handbook-wood as an engineering material. General Technical Report FPL-GTR-190. Madison: U.S. Department of Agriculture, Forest Service, Forest Products Laboratory. DOI: https://doi.org/10.2737/FPL-GTR-190
Slávik, R., Čekon, M. y Štefaňák, J., 2019. A nondestructive indirect approach to long-term wood moisture monitoring based on electrical methods. En: Materials, 12, 2373. DOI: https://doi.org/10.3390/ma12152373
Sotomayor Castellanos, J. R., 2015. Banco FITECMA de características físico-mecánicas de maderas mexicanas [En línea]. Morelia: Universidad Michoacana de San Nicolás de Hidalgo. ISBN: 978-607-00-9036-3. [Consulta: 12 de marzo de 2022]. Disponible en: https://bit.ly/3vkfO60
Suzuki, T., Hasemi, Y., Kamikawa, D., Yasui, N., Kaku, C. y Suzuki, J. I., 2021. Development of dynamic moisture content measurement system for wooden members exposed to fire heating. En: Japan Architectural Review, 4(3), pp.431-441. DOI: https://doi.org/10.1002/2475-8876.12223
Van Blokland, J. y Adamopoulos, S., 2022. Electrical resistance characteristics of thermally modified wood. En: European Journal of Wood and Wood Products, 80, pp.749-752. DOI: https://doi.org/10.1007/s00107-022-01813-7
Xu, H., Li, Q., Xu, Q., Bao, Z., Wang, L. y Xing, T., 2019. Effects of brown-rot decay on the electrical resistance of wood and its mechanism [En línea]. En: BioResources, 14(3), pp.6134-6145. [Consulta: 12 de marzo de 2022]. Disponible en: https://bit.ly/3I8zJfB
Zelinka, S. L., Passarini, L., Colon Quintana, J. L., Glass, S. V., Jakes, J. E. y Wiedenhoeft, A. C., 2016. Cell wall domain and moisture content influence Southern Pine electrical conductivity. En: Wood and Fiber Science, 48, pp.54-61. DOI: https://www.fpl.fs.fed.us/documnts/pdf2016/fpl_2016_zelinka004.pdf
Zhang, J. Y. y Shen, Q., 2019. Processing natural wood into bulk conducting materials. En: SN Applied Sciences, 1(12), 1579. DOI: http://doi.org/10.1007/s42452-019-1572-3


